プレートテクトニクスとマントル対流
10. プレートを持つマントル対流の数値モデル
プレートの運動と沈み込みを作るため,重要な要素は,マントル岩石の流動についての法則と,鉱物の相転移である.この2つのみを実際のマントルに近づけて,ほかの要素は,なるべく簡単にしたモデルを作る.例えば,実際のマントルは三次元の球体である.しかし,実験室の流体のように四角い箱に入ったような流体を考え,図2の手前の面のようにプレートが運動する方向と深さの断面における流れを考える.プレートの運動に垂直な方向の流れは無視する.こういうモデルは二次元モデルと呼ばれる.
2つの重要な要素のうち,1つめの岩石の流動の性質で重要な物は,次の通りである.1番目は, 低温の岩石が高い粘性率を持ち,硬くなることである. 2番目は, 水がプレート間の摩擦を弱める働きをすることである.これら2つに加えて,3番目の性質を考える.岩石はある程度以上強い力を受けると変形しやすくなる.つまり,岩石の粘性率は受ける力が大きくなると低下する性質を持つのである.この性質は,沈み込み帯でプレートが下向きに曲がるときに必要である.これら3つの性質のうち,1番目と3番目の性質は,どの地球型惑星でも持つが,2番目の性質は水のある地球だけが持つ.
ここでは,プレートが沈み込んで滞留スラブを形成する過程を見てみよう.計算はプレートが沈み込む前の温度から出発する.温度が分かると密度と粘性率が計算できるので,流れの速度が計算される.流れに合わせて温度を動かして,さらに,その温度から流れを計算する…ということを繰り返すのである.
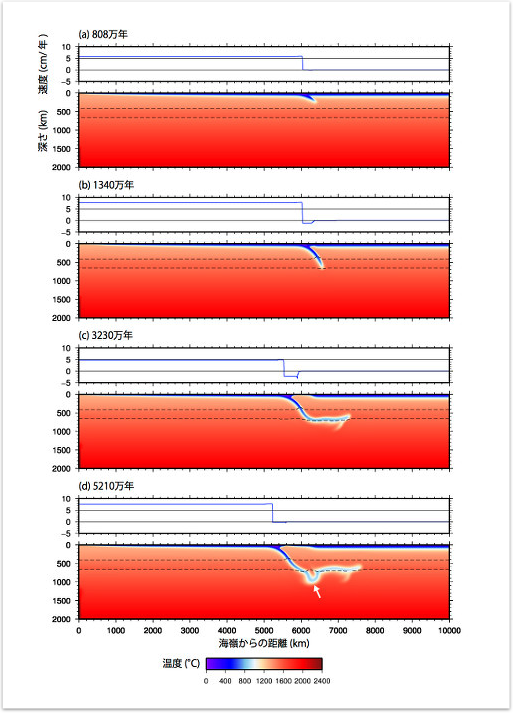
このように計算した結果 (文献11) が,図10である (注34).この図で,左側が沈み込むプレート,右側が,大陸プレートである.プレートの境界には,あらかじめ弱い摩擦を持つ断層を作ってあり,ここから沈み込みが始まる (注35).上の線が,プレートの速度を表す.正の値が,右向きの速度である.速度のグラフから,左側にあるプレートが,右側に向かって動いているのが分かる.つまり,プレートの運動が起きていることを意味する.このモデルでは,プレート運動を再現するのに,プレート境界の摩擦が水の働きによって99%も弱くなると仮定しなければならなかった (注35).すなわち,水の効果はプレートを動かすのに欠かせない物なのである.
下は,色で温度を表している.プレートが沈み込むと,スラブを作る.表面の冷たいところから,垂れ下がっているところである.スラブは徐々に長さを増して行く.2本の点線は深さ410 kmの境界と660 kmの相境界を表している.410 kmと660 kmの相境界をよく見てみよう.スラブがある場所の凸凹のでき方が反対である.410 kmでは上向きに出っ張っているが,660 kmの方は下向きに凹んでいる.これは,660 kmで起きる相転移のクラペイロン勾配が負であるのに対し,410 kmでは正だからだ.このため,410 kmの相境界は660 km相境界と反対の働きをして,スラブを下向きに引っ張る力を増加させる.プレートの運動する速度は,410 kmの相境界を過ぎた後から,急激に増加し,660 kmの境界と接触する前に最大となる.その後は,プレートが動く速度は減少する.
(注34) 4つの図は違う時間の様子を表し,時間は上から下へ経過する.それぞれの時間での上のグラフはプレート運動速度を表す.横軸は海嶺からの距離,縦軸はプレート運動速度であり,単位をcm/年とした.下の図は色で温度を,点線で2つの相境界(深さ410 kmと660 km)を表す.
(注35) どうやって最初の断層を作るのか?ということも問題の1つなのだが,まだ解決されていない問題である.これは,プレートテクトニクスがどのような仕組みで始まったのかという問いに答える鍵である.